Ниже приведен перевод статьи Макалистера и Розенблита "Systematic Nonlinear Planning".

Систематичное нелинейное планирование

Введение

STRIPS-планирование было впервые представлено в статье (Fikes and Nilsson, 1971) как некоторая модель видов задач планирования, для решения которых люди используют разумные рассуждения. STRIPS-планирование соответствует известной формальной задаче поиска на графе. Джон Кенни (John Canny) установил, что формальная STRIPS задача планирования является P-SPACE полной (Canny, 1985). Известно, что NP-полные и P-SPACE полные задачи могут решаться эффективно во многих случаях, встречающихся на практике. Хотя все еще спорно то, что STRIPS-планирование сможет выйти на прикладной уровень при решении больших проблем, становится ясным, что некоторые методы оптимизации поиска могут значительно улучшить производительность алгоритмов планирования.

Процедуры планирования используют три основных подхода для оптимизации процесса поиска. Во-первых, даже ранние системы планирования были "обобщающими" (lifted). Это означает, что они использовали выражения, включающие переменные, такие как, PUTON(A, x), для представления большого количества различных возможных означенных экземпляров, таких как, PUTON(A, B). Ранние планировщики основывались на доказательстве теорем методом резолюций и, поэтому, наследовали их "обобщающую" природу от леммы об обобщении¹ (lifting lemma) (Fikes and Nilsson, 1971) (Robinson, 1965). Во-вторых, будучи обобщающими, большинство современных планировщиков являются также "нелинейными" - они поддерживают частичный порядок шагов плана, а не полный (total) порядок². Этот частичный порядок постепенно уточняется в процессе планирования (Sacerdoti, 1975), (Sacerdoti, 1977), (Tate, 1977), (Chapman, 1987). И, наконец, в-третьих, некоторые планировщики используют "пространства абстракций", в которых планирование сначала выполняется на верхнем уровне абстракции, а затем найденный высокоуровневый план детализируется (Sacerdoti, 1974), (Korf, 1987), (Yang and Tenenberg, 1990).

Нелинейные планировщики иногда называются "планировщики со слабым связыванием". Вообще, неформальный принцип слабого связывания гласит, что выбор более слабого связывания следует делать до выбора более сильного связывания. Обобщение - хороший пример принципа слабого связывания. При поиске плана мы можем выбрать PUTON(A, B) в качестве первого шага плана. Это сильно связанный выбор. Более слабо связанным выбором будет взятие в качестве первого шага выражение вида PUTON(A, x). Нелинейность - другой пример принципа слабого связывания. Вместо выбора выражения вида PUTON(A, x) в качестве первого шага плана, мы можем утверждать, что PUTON(A, x) появится где-то в плане, не указывая точно где.

Данная статья представляет простой, корректный, полный и систематичный алгоритм планирования. Как и большинство ранних планировщиков, наш алгоритм использует обобщение и нелинейность для оптимизации поиска. Наш алгоритм обладает двумя новыми особенностями, которые представлены и обоснованы в этой статье - простота и систематичность. Этот планировщик прост по двум причинам.

Во-первых, процедура (планирования) состоит из двух независимых компонент - простой означенной процедуры и обобщающего метода. Предшествующие алгоритмы планирования конструировались непосредственно как обобщающие процедуры.

Во-вторых, напомним, что Чапмен (Chapman, 1987) показал: любой ЧУ-планировщик должен содержать подпроцедуру для определения так называемого, модального критерия истины, то есть подпроцедуры, которая позволяет определить, истинны ли предусловия шага в незавершенном плане при всех его линеаризациях. (как оказалось, впоследствии Чапмен был неправ) Однако, означенная версия тейтовской процедуры из NONLIN не имеет подобной подпроцедуры, тем не менее она полна и завершенна. Наша означенная процедура является упрощенной версией тейтовской процедуры и также не имеет упомянутой подпроцедуры.

Будучи простой, процедура, представленная здесь, выполняет систематичный поиск, т.е. один и тот же план (никогда не проверяется более одного раза. Систематичность достигается посредством простой модификации означенной версии тейтовской процедуры.

STRIPS-планирование

Сначала мы формально определим задачу STRIPS-планирования, не допуская появления переменных в формулах или в определениях операторов.

Определение: STRIPS-оператор состоит из имени оператора плюс списка предусловий, списка добавления и списка удаления. Элементы списков предусловий, добавления и удаления являются высказываниями, т.е. атомарными полностью-означенными формулами.

Например, в мире кубиков оператор с именем MOVE(A, B, C) (читается "переместить блок A с блока B на блок C") имеет предусловия CLEAR(A), ON(A, B) и CLEAR(C), список удалений ON(A, B) и CLEAR(C) и список добавлений CLEAR(B) и ON(A, C). "Состояние мира" моделируется посредством множества пропозиционных выражений. Дадим стандартное определение результата исполнения STRIPS-оператора в заданном состоянии мира и определение STRIPS проблемы планирования.

Определение: Если o - STRIPS-оператор и S - множество пропозиционных выражений, то если список предусловий оператора o является подмножеством S, то результатом выполнения оператора o в состоянии S является S минус список удалений оператора o плюс список добавлений оператора o. Если список предусловий o не является подмножеством S, то результатом выполнения o в состоянии S будет пустое множество.

Определение: STRIPS задача планирования - это тройка <O, S, G>, где O - множество STRIPS-операторов, S - множество начальных высказываний и G - множество целевых высказываний.

Определение: решением STRIPS задачи планирования <O, S, G> является последовательность операторов из множества O, результатом применения которой к начальному состоянию S будет состояние, содержащее целевое множество G.

Как упоминалось ранее, задача определения, имеет ли решение произвольная STRIPS задача планирования, является P-SPACE полной задачей. В следующем разделе представлена упрощенная означенная версия тейтовской процедуры планирования из NONLIN.

Нелинейное планирование

План - это последовательность операторов. Очевидно, что два плана можно рассматривать как эквивалентные, если один из них может быть выведен из другого посредством переупорядочивания невзаимодействующих шагов. Например, рассмотрим робота, который должен выполнить набор задач в комнате A и набор задач в комнате B. Каждая задача формально ассоциируется с конкретным целевым высказыванием. Мы хотим достичь (сделать истинными) высказывания P₁…P_n, Q₁…Q_m. У нас есть операторы A₁…A_n, B₁…B_m, где A_i действие делает истинным P_i высказывание и при этом должно выполняться в комнате A, а B_i действие делает истинным Q_i высказывание и должно выполняться в комнате B. Более формально, каждое A_i имеет одно предусловие IN(A), добавляет высказывание P_i и не удаляет никаких высказываний. Каждое B_i определяется подобным образом с предусловием IN(B). Пусть у нас также есть оператор GO(A) без предусловий со списком добавления IN(A) и списком удаления IN(B). У нас также есть и аналогичный оператор GO(B). Множество целей {P₁…P_n, Q₁…Q_m} может быть достигнуто (независимо от начального состояния) посредством плана GO(A); A₁;…;A_n; GO(B); B₁;…;B_m. Очевидно, что порядок A_i шагов и порядок B_i шагов не имеет значения, при условии, что все A_i шаги будут выполнены в комнате A, а все B_i шаги - в комнате B. Этот план следует рассматривать как эквивалентный плану GO(A); A_n;…;A₁; GO(B); B_m;…;B₁, в котором шаги A_i и B_i выполняются в обратном порядке. Каждый (линейный) план, который является решением данной проблемы планирования, может быть обобщен "нелинейным планом", который поддерживает только частичный порядок на шагах плана. Два линейных плана рассматриваются как эквивалентные, если они являются разными представлениями одного и того же нелинейного плана.

Чтобы определить нелинейный план, связанный с данным линейным планом, мы сначала должны преодолеть небольшую техническую проблему. В линейном плане мы можем именовать отдельные шаги плана, ссылаясь на них, как на первый шаг, второй шаг и т.д. Однако в нелинейном плане может не быть четко определенного второго шага. Мы также не можем именовать шаги именами операторов, используемых в этих шагах, т.к. несколько шагов могут использовать один и тот же оператор. Для именования шагов в нелинейном плане мы будем полагать, что с каждым шагом ассоциировано отдельное символьное имя, которое называется именем шага.

Определение: таблица символов - это отображение из конечного множества имен шагов в операторы. Каждая таблица символов должна содержать два особенных имени шага, называемых START и FINISH. START отображается на некий фиктивный оператор, который не имеет предусловий и списка удалений, но добавляет множество "начальных высказываний". Аналогично, FINISH отображается на оператор, который имеет множество предусловий, называемых "целевыми формулами", но имеет пустые списки добавления и удаления.

Отметим, что таблица символов не налагает упорядочивающих ограничений на имена шагов. Отметим также, что имена шагов отличны от имен операторов. Два имени шага, скажем STEP-37 и STEP-52, могут оба отображаться на оператор, именуемый MOVE(A, B, C). Отметим также, что шаг STEP-37 не обязательно должен предшествовать STEP-52 - имена шагов не имеют никакого другого значения, кроме идентификатора (place holder) шага в плане.

Рассмотрим (линейное) решение (solution) STRIPS задачи планирования. Очевидно, что каждое предусловие каждого шага в плане-решении истинно, когда этот шаг выполняется. Если w - имя шага и P - предусловие w, то должен существовать некий "источник" (source) P для w - хотя источником может служить и виртуальный шаг START. Если каждое предусловие выполняется для каждого оператора в плане, то каждое предусловие P каждого шага имеет уникальный источник - последний предшествующий шаг, который добавил P. Это касается и предусловий виртуального шага FINISH, т.е. целевых формул. Понятие источника послужило причиной введения понятия причинной связи.

Определение: Причинная связь - это тройка <s, P, w>, где P - высказывание, w - имя шага, который содержит P в списке предусловий и s - имя шага, который содержит P в списке добавления. Причинная связь записывается в виде s-P—>w.

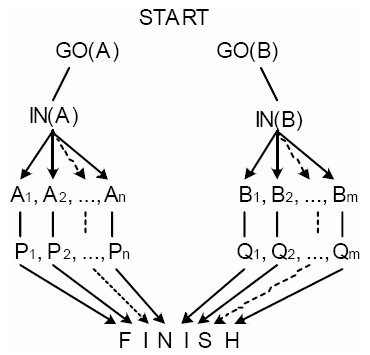
Причинные связи отражают зависимости между шагами плана. Причинную связь следует рассматривать как ограничение. Причинная связь s-P—>w требует, чтобы шаг s предшествовал шагу w, и чтобы не было шагов между s и w, которые добавляют или удаляют P. Для любого заданного линейного плана можно извлечь причинные связи этого плана. Например, рассмотрим план GO(A); A₁;…;A_n; GO(B); B₁;…;B_m, упоминавшийся ранее. Этот план имеет множество причинных связей, отраженных на рисунке 1. К сожалению, причинные связи отражают не все релевантные упорядочивающие ограничения в этом плане. Информация о частичном порядке, скрытая в причинных связях, не требует, чтобы все Ai были выполнены до GO(B). Этот пример показывает необходимость упорядочивающей информации, отличной от причинных связей⁴.

Рисунок 1: Причинные связи в линейном плане GO(A); A1;…;An; GO(B); B1;…;Bm

Определение: Имя шага v называется угрозой (threat) для причинной связи s-P—>w, если v - имя шага, отличное от s и w, которое добавляет или удаляет P.

Определение: Условие сохранности - это отношения порядка s<w или w>s, где s и w - имена шагов.

В плане, показанном на рисунке 1, шаг GO(A) является угрозой для всех причинных связей вида GO(B)-IN(B)—>B_i (т.к. GO(A) удаляет высказывание IN(B)), ведущей к условию сохранности GO(A) < GO(B). Аналогично, шаг GO(B) является угрозой для всех причинных связей вида GO(A)-IN(A)—>A_i, приводя к условиям сохранности вида A_i < GO(B). Эти условия сохранности вместе с отношениями порядка, скрытыми в причинных связях, допускают выполнение шагов в любом порядке, в котором GO(A) предшествует каждому A_i, каждое A_i предшествует GO(B) и GO(B) предшествует каждому из B_i.

Определение: Нелинейный план состоит из таблицы символов, множества причинных связей и множества условий сохранности.

Определение: Нелинейный план называется завершенным (complete), если выполняются следующие условия:

1. каждое имя шага, присутствующее в причинной связи или условии сохранности, имеет запись в таблице символов;
2. если w - имя шага в таблице символов и w имеет предусловие P, то план содержит причинную связь вида s-P—>w;
3. если план содержит причинную связь s-P—>w и в таблице символов есть имя шага v, который является угрозой каузальной связи s-P—>w, то план содержит либо условие сохранности v<s, либо условие сохранности v>w.

Можно показать, что любое (линейное) решение STRIPS проблемы планирования соответствует нелинейному плану, который является наименьшим (наименьшее число причинных связей и условий сохранности) завершенным нелинейным планом, соответствующим данному линейному плану. Эта "нелинейное обобщение" данного линейного плана является уникальной вплоть до произвольного выбора имен шагов. Нелинейное обобщение линейных планов определяет отношение эквивалентности на линейных планах - два линейных плана эквивалентны, если они имеют одно и то же нелинейное обобщение.

Определение: Топологической сортировкой нелинейного плана является линейная последовательность всех имен шагов в таблице символов такая, что выполняются следующие условия:

1. первым шагом в последовательности будет START;
2. последним шагом в последовательности будет FINISH;
3. для каждой причинной связи s-P—>w в плане шаг s предшествует шагу w;
4. для каждого условия сохранности u<v (или v>u) в плане шаг u предшествует шагу v.

Определение: топологическая сортировка нелинейного плана является решением, если выполнение последовательности операторов шагов между шагами START и FINISH, начиная с состояния, заданного в списке добавление шага START, приведет к состоянию, которое содержит все предусловия шага FINISH.

Лемма: Любая топологическая сортировка завершенного нелинейного плана является решением.

Можно написать процедуру планирования, которая систематично ищет в пространстве нелинейных планов. Поиск называется систематичным в техническом смысле, если он никогда не рассматривает один и тот же план, или даже эквивалентные планы, дважды - каждая ветвь дерева поиска делит оставшиеся возможности на непересекающиеся множества возможных решений так, что все эквивалентные планы находятся под той же веткой дерева поиска. Однако прежде, чем определить процедуру, требуется одно дополнительно определение.

Определение: Нелинейный план (не обязательно завершенный) называется порядко-противоречивым (order inconsistent), если он не имеет топологической сортировки.

Алгоритм транзитивного замыкания может быть использован для определения, является ли данный нелинейный план порядко-противоречивым. Нелинейный план является порядко-противоречивым, если и только если причинные связи и условия сохранности плана образуют цикл на множестве шагов плана.

Наша процедура поиска является процедурой поиска в глубину с ограничением, которая может использоваться с повторяющимся углублением (Korf, 1985). Процедура принимает в качестве параметров (частичный) нелинейный план и ограничение стоимости (cost bound) и ищет завершение (completion) данного плана, так чтобы общая стоимость шагов в завершенном плане не превосходила заданного ограничения стоимости. Изначально процедура вызывается с (частичным) нелинейным планом, который содержит только шаги START и FINISH, соответствующие заданной STRIPS задаче планирования. Мы также полагаем, что заданы допустимые операторы.

Можно проверить, что каждое завершение (completion) данного плана со стоимостью меньшей либо равной cost_bound эквивалентно (с точностью до имен шагов) возможному результату вышеприведенной процедуры. Более того, можно показать, что не существует двух различных путей исполнения процедуры, которые могут породить эквивалентные завершенные планы. Чтобы продемонстрировать это, отметим, что каждый шаг плана может быть уникально именован, начиная с шага FINISH и продвигаясь назад по причинным связям с отметкой предусловий каждой связи. Это значит, что каждый шаг может быть уникально идентифицирован способом, независимым от имен шагов. Поэтому невозможно сгенерировать два эквивалентных плана путем различных означиваний s в шагах 4a и 4b алгоритма. Это также означает, что упорядочивающие ограничения v<s и v>w, используемые на шаге 3, могут быть определены независимо от имен шагов. Это означает, что завершения (completion), удовлетворяющие v<s, не могут быть эквивалентны (с точностью до имен шагов) завершению, удовлетворяющему v>w. Таким образом, вышеприведенная процедура, представляет систематичный поиск в пространстве завершенных нелинейных планов.

Комментарии к процедуре

Хотя процедура, приведенная в предыдущем разделе, является, по существу, упрощением тейтовской процедуры из NONLIN, существует одно техническое отличие, достойное упоминания. Тейтовская процедура использует другое понятие угрозы, при котором v рассматривается как угроза связи s-P—>w, только если v удаляет P. Более строгое понятие, используемое здесь, (при котором v считается угрозой связи s-P—>w, если v либо добавляет, либо удаляет P) необходимо для систематичности. Тейтовское понятие угрозы допускает случаи, когда два отдельных завершенных нелинейных плана имеют общую топологическую сортировку. В этом случае линейные планы не имеют уникальных нелинейных абстракций. Однако кажется возможным, что тейтовское слабое определение угрозы работает столь же хорошо на практике, если не лучше.

Процедура, приведенная в предыдущей секции, может быть модифицирована для поддержки планирования в ряде пространств абстракций. Предположим, что для каждого пропозиционного выражения задается число, выражающее его "абстрактность". Мы хотим быть уверены, что абстрактные предусловия будут удовлетворены до того, как мы попытаемся удовлетворить некоторые другие предусловия. Шаги 3 и 4 процедуры выбирают либо предусловие, которое еще не связано причинной связью, либо угрозу к существующей причинной связи. Выбор предусловия или находящейся под угрозой причинной связи можно выполнять произвольным образом. Практически, этот выбор может быть выполнен способом, который максимизирует абстрактность связанных предусловий. Если это так, то процедура будет рассматривать конкретные предусловия только после того, как будут рассмотрены все более абстрактные. Очевидно, что следует рассматривать "сложные" предусловия до рассмотрения "простых".

Лемма в предыдущей секции утверждает, что каждый завершенный нелинейный план является безопасным (safe) в смысле, что каждая топологическая сортировка плана является решением. Однако, обратное не верно. Существует безопасный частичный порядок шагов плана, который не соответствует какому-либо завершенному нелинейному плану. Рассмотрим, например, частичный порядок шагов плана, изображенный на рисунке 2⁶. В этом плане FINISH имеет предусловия P, Q и R. Шаг w₁ добавляет P и Q, а шаг w₂ добавляет P и R. Шаг w₁ имеет предусловие W₁, которое добавляется шагом s₁, а шаг w₂ имеет предусловие W₂, которое добавляется шагом s₂. К сожалению, оба шага s₁ и s₂ удаляет P. Частичный порядок шагов плана, показанный на рисунке, является безопасным. Однако, любой завершенный план (по определению, данному в этой статье) должен определять, который из шагов w₁ или w₂ является причинным источником (source) предусловия P шага FINISH. Это повлечет явное упорядочение шагов w₁и w₂.

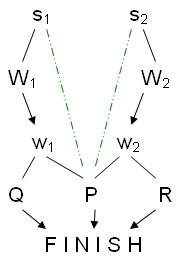Рисунок 2: Безопасный, но частичный нелинейный план

Можно систематично искать все частичные порядки на именах шагов и найти наиболее абстрактный (с наименьшей связностью) частичный порядок, который будет безопасным. К сожалению, кажется, не существует способа сделать это эффективно. Вычисление чепменовского критерия модальной истинности в каждом узле пространства поиска вычислительно очень дорогостоящая операция. Более того, рассмотрение модального критерия истины как недетерминированной процедуры так, как это сделано в TWEAK, нейтрализует систематичность поиска. Это обусловлено тем, что выборы при использовании модального критерия истины (дизъюнкции и кванторы существования) не согласуются с делением пространства частичных порядков на непересекающиеся множества (один и тот же частичный порядок может достигаться в различных ветвях дерева поиска). Даже если бы можно было организовать систематичный поиск в пространстве частичных порядков на множестве имен шагов, различные порядки имен шагов могли бы соответствовать одному и тому же порядку настоящих операторов. Это значит, что в отличие от процедуры, приведенной здесь, поиск все равно не будет систематичным поиском последовательности операторов.

Обобщение (lifting)

Обобщение было предложено Робинсоном вместе с методом резолюций для доказательства теорем (Robinson 1965). В настоящее время обобщение - стандартная технология построения новых алгоритмов доказательства теорем и переписывания термов (term rewriting)⁷. Применение обобщения связано с леммой об обобщении (lifting lemma), которая гласит, что для каждого допустимого вычисления (computation), включающего означенные выражения, существует обобщенное вычисление, использующие переменные, таким образом, что означенные вычисления являются частным случаем обобщенных вычислений.

Процедура, приведенная выше, создана для означенного случая - случая, когда формулы в списках предусловий, добавлений и удалений оператора не содержат переменных. Эта процедура может быть обобщена (lifted) для работы со схемами операторов и планами, включающими переменные. Обобщающая трансформация, используемая здесь, является довольно общей, и применима к большому классу недетерминированных программ.

Для обобщения процедуры из предыдущей секции отметим сначала, что процедура уже может работать со схемами операторов в том виде, в каком она представлена выше. Схема оператора - это оператор, в котором переменные присутствуют в имени оператора, а также в списках предусловий, добавлений и удалений. Например, в мире кубиков с n кубиками существует n³ операторов вида MOVE(A, B, C)⁸. Эти n³ различных операторов являются лишь различными экземплярами (означиваниями) одной схемы оператора MOVE(x, y, z), которая содержит переменные x, y и z. Чтобы использовать процедуру из предыдущей секции со схемами операторов вместо означенных операторов, шаг 4b нужно изменить следующим образом:

4b. Пусть o_i - некоторый означенный экземпляр схемы оператора. If P не является членом списка добавления оператора o_i, then fail. Иначе, создаем новую запись таблице символов, которая отражает новое имя шага s на оператор o_i. ...

Эта версия шага 4b все еще является означенной процедурой. Отметим, что недетерминированная степень ветвления этого шага является бесконечной - если произвольные термы могут быть использованы в операции подстановки, то существует бесконечно много означенных экземпляров одной схемы оператора. Ясно, что это неприемлемо для практического планирования. Чтобы обобщить означенную процедуру, мы заменим шаг 4b предложенный ранее следующим.

4b. Пусть o_i - копия, с новыми переменными, одной из имеющихся схем операторов. If P не является членом списка добавления o_i, then fail. Иначе, создаем новую запись таблице символов, которая отражает новое имя шага s на копию схемы o_i. ...

Отметим, что только первая часть шага изменилась. Степень ветвления первой части обобщенного шага 4b эквивалентна количеству различных схем операторов - в случае мира кубиков, есть только одна схема, так что шаг вообще является детерминированным. Остальная часть обобщенной процедуры идентична процедуре, приведенной в предыдущем разделе. Однако в обобщенной версии процедуры выражения могут содержать переменные. Проверку эквивалентности между двумя выражениями, которые содержат переменные, следует рассматривать как недетерминированную операцию. Проверка эквивалентности может возвращать истину, в этом случае генерируется "ограничение эквивалентности". Проверка эквивалентности может возвращать ложь, в этом случае генерируется ограничение неэквивалентности. Например, вторая часть шага 4b читается, как "Если P не является членом списка добавление o_i, то провал". Чтобы определить, является ли P членом списка добавления o_i, мы можем написать простую рекурсивную проверку, которая выполняет проверку эквивалентности между высказыванием P и каждым из членов списка добавления o_i. Каждая проверка эквивалентности может возвращать либо истину, либо ложь. Выполнение алгоритма продолжается, только если какая-либо из проверок эквивалентности возвращает истину, и, следовательно, порождает отношение эквивалентности между P и элементом списка добавления o_i. Ограничения эквивалентности приводят к унификации. Если отношение эквивалентности порождено для выражений, которые не могут быть унифицированы, то эта ветвь недетерминированных вычислений отсекается (fail). Следовательно, такая версия шага 4b выполняется, только если P согласуется с некоторым элементом списка добавления o_i.

Обобщающая трансформация заменяет все утверждения вида "пусть x - означенный экземпляр схемы y" на "пусть x - копия y с новыми переменными". Каждая проверка эквивалентности рассматривается как недетерминированная операция, которая либо возвращает истину и порождает отношение эквивалентности, либо возвращает ложь и порождает отношение неэквивалентности. Если множество отношений эквивалентности и неэквивалентности когда-либо становится противоречивым, то эта ветвь недетерминированных вычислений обрывается. Если дано такое множество ограничений эквивалентности и неэквивалентности на множестве выражений, включающих переменные, то можно легко определить, выполняются ли ограничения. Если быть более точным, сначала к ограничениям эквивалентности применяется алгоритм унификации, чтобы проверить, могут ли эти ограничения выполняться одновременно. Если унификация завершится успешно, то применяется подстановка во все выражения, вытекающая из унификации. Если существует отношение неэквивалентности между двумя выражениями, которые стали одним и тем же выражением в результате подстановки, то ограничения невыполнимы. В ином случае, ограничения выполнимы. На практике, операцию унификации следует выполнять постепенно по мере того, как генерируются ограничения эквивалентности.

Заключение

Существовавшие до настоящего времени нелинейные алгоритмы планирования были весьма сложны и не были систематичными. Используя обобщение, как отдельный метод оптимизации, который может создаваться после того, как основной алгоритм сконструирован, мы получили простую, корректную и полную, систематичную обобщающую нелинейную процедуру.

Список литературы

-------------------

[1] В отечественной литературе часто встречается также перевод "лемма о подъеме". [прим. переводчика]

[2] Это предложение является примером терминологической путаницы, возникшей между понятиями "нелинейный планировщик" и "планировщик, поддерживающий частичный порядок шагов в плане (POP)". В предложении речь идет как раз о втором типе планировщиков. Далее по тексту термин "нелинейный планировщик" следует понимать именно как "POP-планировщик", а "нелинейность" - как "частичное упорядочивание шагов (действий)". [прим. переводчика]

[3] В оригинале используется термин "незавершенный план" (incomplete plan). Мы будем пользоваться более распространенной в настоящее время терминологией и при переводе употреблять термин "частичный план" (partial plan) вместо "незавершенный план". [прим. переводчика]

[4] Тейт использует термин "диапазон" (range) вместо причинной связи.

[5] С практической точки зрения в качестве компонента начального частичного плана процедуре полезно также передавать ограничение START < FINISH. Кроме того, при добавлении очередного шага S в план полезно сразу добавлять ограничения (START < S) и (S < FINISH). [прим. переводчика]

[6] Этот пример предложен Subbarao Kambhampati.

[7] Затрудняюсь перевести термин на русский язык. Близко по смыслу к "символьному выводу по правилам", т.е. когда в соответствии с некоторым набором правил одни символы (термы) в выражении (строке) заменяются на другие. Более подробно см. encyclopedia.thefreedictionary.com [Term rewriting]. [прим. переводчика]

[8] Авторы указали неверную формулу для расчета количества операторов MOVE для n кубиков. Нужно считать количество размещений n кубиков по трем аргументам MOVE. Количество размещений n по 3 равно n!/(n-3)!. [прим. переводчика]

На русский язык статью перевел Трофимов И.В.

август 2005 г